----------- Your trusted source for independent sensor data- Photons to Photos------------ Last revised: 2021-06-10 13:00 GMT-5

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article

-------------------------- Optics Primer - Projection Classification

--------------------------------------------------------- By Bill Claff

Lenses project images, usually onto an image plane, sometimes onto a curved surface. I will assume only image planes in this article.
The way the image is projected is classified according to where rays of an incoming angle are projected onto the image.
The angle of the incoming ray ranges from zero on the optical axis to the half-angle of view of the lens.
I will use Θ to indicate that angle. Since optical prescriptions generally use ω to indicate the half-angle of view this means that 0 <= Θ <= ω.
And I will use y to indicate how far from the optical axis the ray arrives at the image plane although you may see the letter r (for radius) elsewhere.
Optical prescriptions specify image height as Y so my choice reminds us that 0 <= y <= Y.
Naturally, in any of the following formulas f indicates focal length.

The projections follow trigonometric functions that I will list in the following table.
These formulas are often shown in terms of y (or r) but I prefer to restate them in terms of (y / f).

	y =	(y / f) =
Rectilinear	f tan( Θ )	tan( Θ )
Stereographic	2 f tan( Θ / 2 )	2 tan( Θ / 2 )
Equidistant	f Θ	Θ
Equisolid angle	2 f sin ( Θ / 2 )	2 sin ( Θ / 2 )
Orthographic	f sin ( Θ )	sin ( Θ )

You might protest that the Equidistant formula is not trigonometric.
However, note that both k * tan ( Θ / k ) and k * sin ( Θ / k ) approach Θ as k approaches infinity.

It's useful to look at these projection formulas graphically:

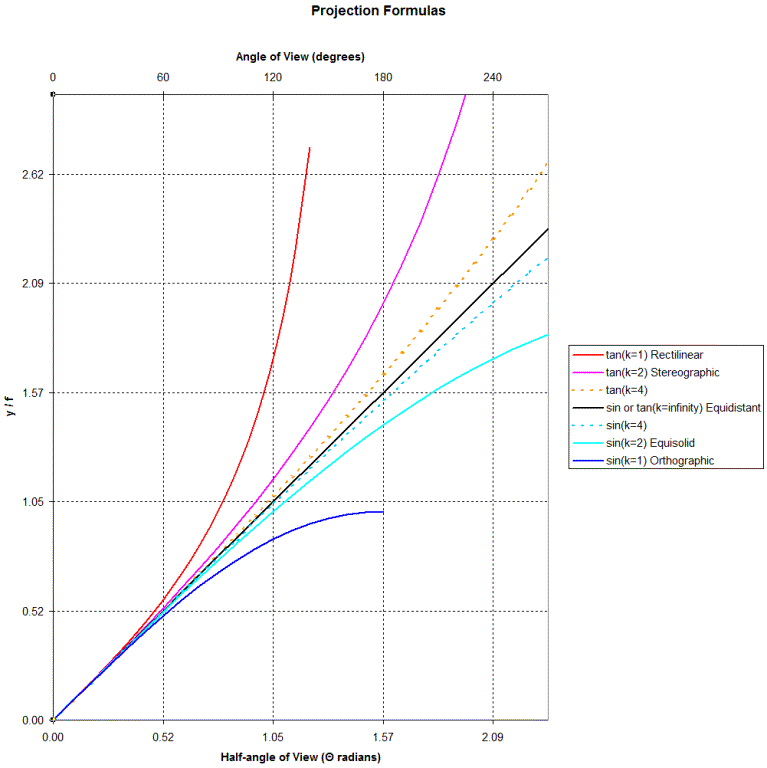
I limited the y-axis of this chart so I could better maintain the proper aspect ratio. Notice that when the y-axis is y / f the Equidistant line has a slope of 1.
The x-axis is limited to an angle of view of 270 degrees which is the largest angle of view for which I have ever seen an optical prescription.
And the Rectilinear line is limited to an angle of view of 140 degrees which exceeds the angle of view of the widest rectilinear lens that has been produced.

I don't think of these projections as distinct but rather as members of two families of curves that meet at the Equidistant (also Equiangular) line.
Above the Equidistant line we have k * tan ( Θ / k ) and below that line k * sin ( Θ / k ).

To give the reader a sense for how quickly these families converge on the Equidistant line I added curves for 4 * tan ( Θ / 4 ) and for 4 * sin ( Θ / 4 ).

No lens follows a projection formula perfectly. In a separate article we'll learn more about where the boundary between Rectilinear and the other projections actually lies.
For now simply note that below the Rectilinear line is barrel distortion and above it is pincushion distortion.
Also, consider this; when the angle of view is small the projections are indistinguishable.
So we might label a telephoto lens as Rectilinear but it might be indistinguishable from even Orthographic!

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article