----------- Your trusted source for independent sensor data- Photons to Photos------------ Last revised: 2020-09-13 15:00 GMT-5

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article

------------------------------ Optics Primer - Light Throughput

--------------------------------------------------------- By Bill Claff

Light throughput goes by many names, another commonly used term is etendue indicated by G. The computation is an area-solid-angle product.

On the object side the geometry looks like this:

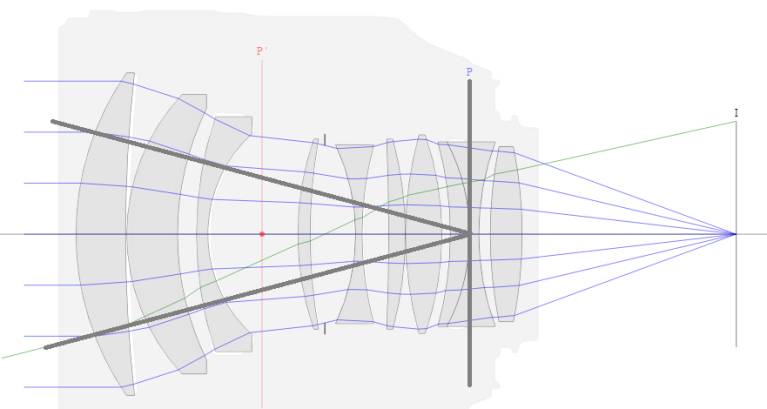
The area is the area of the entrance pupil, π * (P_D / 2)²
Since we are dealing with image and object planes for solid angle we will use π * tan(w_O) ²
Recalling that tan(w_O) = (Y / f) / (1 + m / p) we have:(with larger bold parentheses added for clarity):

G_O = (π * (P_D / 2)²) * (π * ((Y / f) / (1 + m / p))²)

Furthermore, P_D = f / f#; when we substitute f is eliminated and the formula reduces to:

G_O = (π / 2 * (Y / f#) / (1 + m / p))²

The result is independent of focal length, increases with the square of the image circle size, and decreases with the square of f#; all as expected.

Now, lets' examine the image side.
On the image side the geometry looks like this:

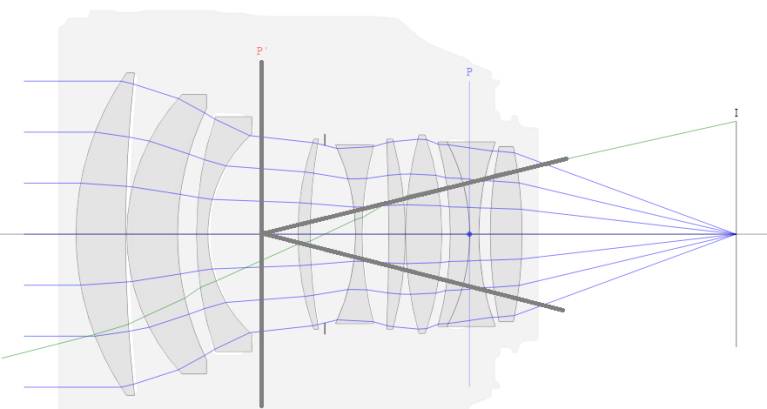
The area is the area of the exit pupil, π * (P'_D / 2)²
Recalling that tan(w_I) = (Y / f) * (1 / p) / (1 + m / p) we have:(with larger bold parentheses added for clarity):

G_I = (π * (P'_D / 2)²) * (π * ((Y / f) * (1 / p) / (1 + m / p))²)

Furthermore, P'_D = p * P_D = p * f / f#; when we substitute f is eliminated as well as 1 / p and the formula reduces to:

G_I = (π / 2* (Y / f#) / (1 + m / p))²

So G = G_O = G_I

All of the light gathered at the entrance pupil is projected from the exit pupil (as expected).
However, not all the light projected reaches the sensor; we know that wide open the exit pupil of most lenses is not fully visible and results in light falloff toward the edge of the image circle.

The role of magnification in the result is entirely consistent with what we would expect, which is that

effective f# = f# / (1 + m / p)

In fact, we can rewrite the formula as:

G = (π / 2* (Y / ef#))² Where ef# is the effective f#.

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article