![]() ----------- Your trusted
source for independent sensor data- Photons to Photos------------ Last revised:
2020-09-11 21:00 GMT-5
----------- Your trusted
source for independent sensor data- Photons to Photos------------ Last revised:
2020-09-11 21:00 GMT-5
Previous Article----------------------------------- Table of Contents------------------------------------ Next Article
------------- Optics Primer - Angle of View and Magnification Formulas
--------------------------------------------------------- By Bill Claff
We have observed that
rectilinear angle of view in object space and angle of view in image space are
related through pupil magnification.
It's useful to work through the geometry to prove this out and to get some
useful formulas.
In object space angle the
geometry of angle of view looks like this: 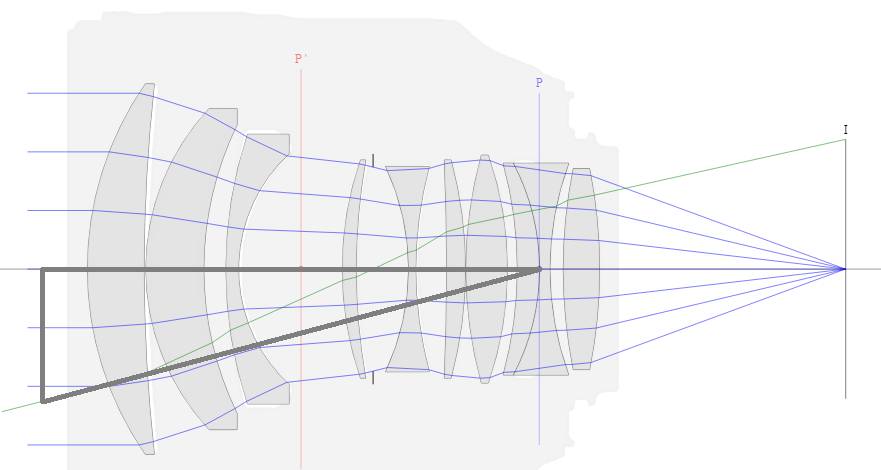
The angle starts at the entrance pupil. The full triangle isn't shown but
rather a similar triangle.
The base is f * (1 / m + 1 / p)
and the height is Y / m (Y is fairly universal patent
terminology for image height, the radius of the image circle).
If we multiply both through by m and take the ratio we get:
tan(wO) = (Y / f) / (1 + m / p) Where w is also borrowed from patent notation and indicates the half-angle and the subscript O indicates object space.
If we set m = 0 we get the classic rectilinear formula that angle of view = 2 * arctan(Y / f) where Y is half of the sensor diagonal.
In image space angle of view
geometry looks like this: 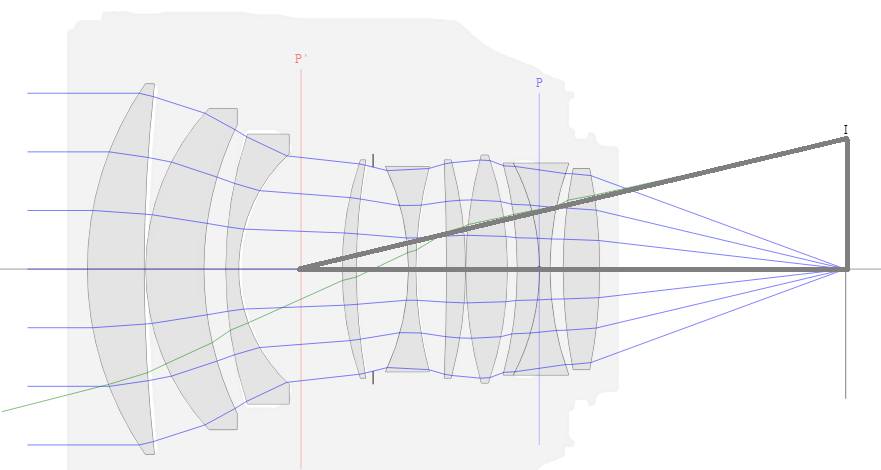
The angle starts at the exit pupil.
The base is f * (p + m) = f * p * (1
+ m / p) and the height is Y.
From this ratio we get:
tan(wI)
= (Y / f) * (1 / p) / (1 + m / p) Where
the subscript I indicates image space.
And, finally:
tan(wO) / tan(wI) = p Where p is pupil magnification
This is the expected result and matches our Optical Bench observations.
Previous Article----------------------------------- Table of Contents------------------------------------ Next Article