----------- Your trusted source for independent sensor data- Photons to Photos------------ Last revised: 2020-09-11 17:00 GMT-5

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article

---------------------------- Optics Primer - Bokeh Ball Diameter

--------------------------------------------------------- By Bill Claff

The term bokeh refers to the quality of out of focus blur. Most aspects of bokeh are subjective rather than objectively measurable.
One attribute of bokeh that can be measured is the diameter of the bokeh ball, the blur circle.
We use the term circle loosely as we do in other areas such as Circle of Confusion (CoC) since away from the optical axis the effect is not necessarily circular.

Bokeh is closely related to Depth of Field (DoF) and we can rearrange out DoF equations to predict bokeh ball diameter, B:

B = P_D * (m_n - m) / (1 + m_n / p) When bokeh magnification (m_n) is larger than in focus magnification (m)

B = P_D * (m - m_f) / (1 + m_f / p) When bokeh magnification (m_f) is smaller than in focus magnification (m)

Or unified as:

B = P_D * |m - m_b| / (1 + m_b / p) Where bokeh magnification is m_b and in focus magnification is m.

In these equations P_D is entrance pupil diameter and p is pupil magnification (P'_D / P_D) where P'_D is exit pupil diameter.

Bokeh magnification, m_b, is the magnification that the object creating the blur circle would have if it were in focus.

As with depth of field I'll keep the equations in terms of magnification knowing we can always convert to subject distance as needed with the equation:
S = ( 1 / m + 1 ) * f + i + ( 1 + m ) * f where f is focal length and i is the internodal distance

We generally see bokeh balls rather than a continuous blur when there is a small bright object whose blur disc stands out from others nearby.

In most photography bokeh balls are behind the in focus subject; they are less magnified. This isn't a requirement but simply a common composition.

The unified equation is a bit unwieldy. One straightforward simplification we can usually make is that m_b is much smaller than p.
This makes p moot and we get the simplified equation:

B = P_D * |m - m_b|

In many conversations regarding bokeh ball size this is then over-simplified to assume that the objects inducing bokeh are so far in the background as to be considered at infinity; that m_b is zero.

B = P_D * m

Another difficulty is that many people have trouble thinking about magnification as opposed to distance.
So, we can reintroduce non-infinity and switch to distance by returning to the simplified equation and using S = f / m as an approximation to the full distance equation.
So with m = f / S we get:

B = P_D * |m - m_b| = P_D * |f / S - f / S_b| = P_D * f |1 / S - 1 / S_b| = P_D * f |(S_b - S) / (S * S_b)|
And finally:

B = P_D * m |(S_b - S) / S_b| = P_D * m |1 - S / S_b|

In other words we can adjust the blur diameter computed at infinity by:

|1 - S / S_b| Where S is the in focus distance and S_b is the distance to the bokeh.

For example, if the in focus subject is at 10m and the background producing bokeh is at 40m then the blur B is |1 - 10m / 40m| = 0.75 times the blur using the infinity assumption.

If we keep the subject at 10m and the background producing the bokeh as at 25m then the blur B is |1 - 10m / 25m| = 0.60 times the blur using the infinity assumption.

So, the proportion of these magnifications (distances) is relevant to bokeh ball size.

This topic isn't so conducive to the Optical Bench so I gathered some data from actual photographs.

My first test was with a Nikon AF Nikkor 50mm f/1.8D. I chose this lens because it focuses entirely by extension so changing focus is entirely equivalent to changing distance.
I provoke bokeh balls by taking a series of images of miniature white Christmas lights. In taking the images I tried to move the focus ring equally between each shot.
Here is a mosaic of crops taken from those images:

If you click you'll get to view a larger version if you like.

The images are arranged from infinity to closest focus and we can clearly see the bokeh ball get smaller until it is approximately in focus in the 4th image and then get larger (and dimmer) as magnification increases.

I measured the bokeh ball sizes and assigned magnification equally from zero to maximum for the lens since I had advanced the helicoid (almost) equally between each shot.
For such a crude test the results were surprisingly good and consistent with what we would expect:

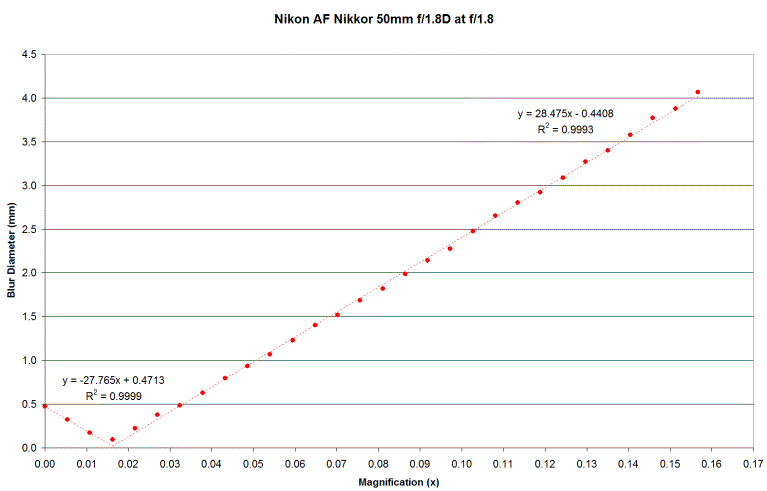
Remember that blur as a function of m is B = P_D * |m - m_b| / (1 + m_b / p)
So with m_b much less than 1 we would expect the slope to be approximately P_D = 50mm / 1.8 = 27.777mm; and it is.
And we would expect the dotted fit lines to meet at a blur diameter of zero for the in focus image; as they do.

I repeated this experiment with a relatively large aperture lens with internal focus with similar results.
I assigned magnification based on subject distance from the metadata and solving the subject distance formula for m.:

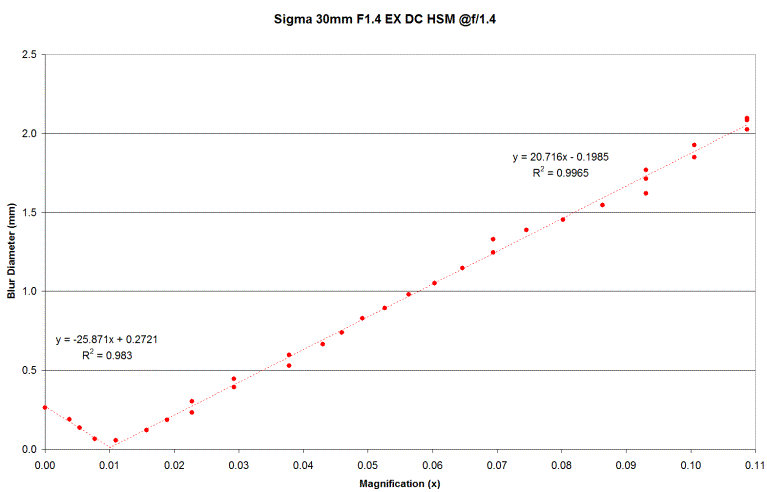
Again, the slope is approximately 30mm / 1.4 = 21.429mm; as expected.

Slightly off the topic, but so long as we are here, note the following crops of bokeh balls (from the 30mm lens):

The red and green rings are from longitudinal chromatic aberration; red when the bokeh ball is in front of the focus and green when it is behind.
Also, the concentric "onion" appearance is due to slight imperfections normally associated with aspherical elements.

If we took images more stopped down then we would start to see the shape (blades) of the iris rather than such round images.

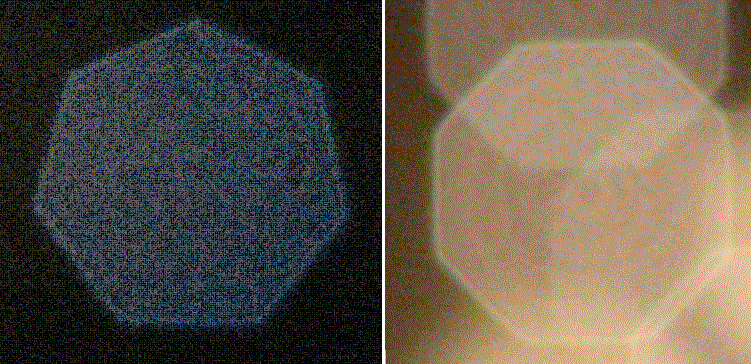
50mm (7 blades not aspherical) on the left and 30mm (8 blades aspherical) on the right.

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article