Circle of Confusion
Prepared 2006-06-28 by Bill Claff
Circle of Confusion
The Circle of Confusion (
) is the diameter of a circle on film or sensor that serves
as the upper threshold for acceptable focus.
Note that the term focus is chosen carefully and is not to be confused with
sharpness.
An image can be in perfect focus and not appear sharp due to reasons unrelated
to 
.
is an important
photographic concept that is used in a number of areas, most notably as part of
the calculation of Depth Of Field (DOF).
The treatment of 
in this article is
somewhat unusual but is consistent with write-ups and results you may have seen
elsewhere.
The value of 
depends on three
factors:
1. The visual acuity of the human eye.
2. The viewing distance to the print or projected image.
3. The enlargement factor that was used to produce the print or projected image.
For the balance of this article I will use the term print
rather than the more wordy print or projected image.
However, it is understood that the same principles apply to projected images as
to prints.
Visual Acuity of the Human Eye
As with any human characteristic visual acuity varies from
person to person.
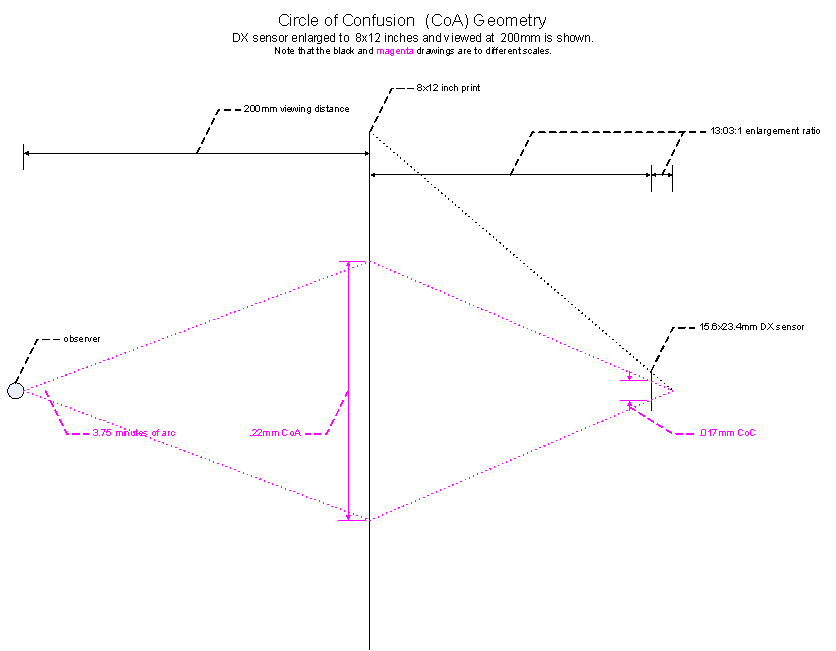
For the purposes of this article I will use 
to denote this
quantity and a value of 3.75 minutes of arc.
Viewing Distance
As viewing distance (
) increases, the cone this is formed by the visual acuity of
the human eye expands.
Let's call this quantity the Circle of Acuity (
).
By simple trigonometry:
Note that for the value of 
we are using that 
(for small angles 
.)
I'll use the value of .0011, which is within 1% of the "exact" value for
computational simplicity.
At a "typical" hand-held distance of 200mm (nearly 8 inches),
and
.
Enlargement Factor
Usually some amount of enlargement is required to form a print
from film or a digital sensor.
I have chosen the term enlargement and avoided the term magnification because
magnification has a very specific meaning in the context optics and close-up
photography.
Let's call enlargement 
and by similar
triangles:
In the "trivial" case of an 8x10 inch large format negative
and an 8x10 inch print, 
and 
.
So at a "typical" hand-held viewing distance of 200mm, 
.
This agrees with the commonly cited value for 8x10 inch film.
.
and 
.
and 
.
and 
.
and 
value.
by 
;
values computed above
would drop from between .017mm and .020mm to .013mm and .015mm respectively.
is required if we
intend to display 20x30 inch (508x762mm) uncropped prints from a DX sensor to
be viewed at a distance of 24 inches?
, 
, and 
) is straightforward and intuitive.
is indispensable in
choosing an aperture for desired Depth Of Field (DOF), and estimating exposure
times at avoid camera shake.