----------- Your trusted source for independent sensor data- Photons to Photos------------------------ Last revised: 2017-01-30

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article

---- Sensor Analysis Primer - An Introduction to 2D Fourier Transforms for Sensor Analysis

--------------------------------------------------------- By Bill Claff

Introduction

The Fourier Transform (FT) can be used a number of ways to analyze and process images.
In this article we'll concentrate on the narrow topic of 2D FTs as applied to sensor analysis.
If you want to play with FT yourself a good place to start is with ImageJ.

Note that many authors, including myself when I slip up, will use the acronym FFT rather than FT.
FFT stands for Fast Fourier Transform and is an algorithm commonly used to compute FTs.

Roadmap

I am going to present a number of synthetically generated images that represent our understanding of what we ought to observe.
In each case the image will be presented on the left and the 2D FT for that image on the right.
The left-hand images are linked to PGM files so you can play with them yourself.
(You will want to use Save link as ... rather than Save image as ... to get the PGM otherwise you'll get a JPG.)
The style of PGM file provided can be opened in ImageJ as well as any text editor or even Excel.

Here's a diagram of the roadmap I will follow:

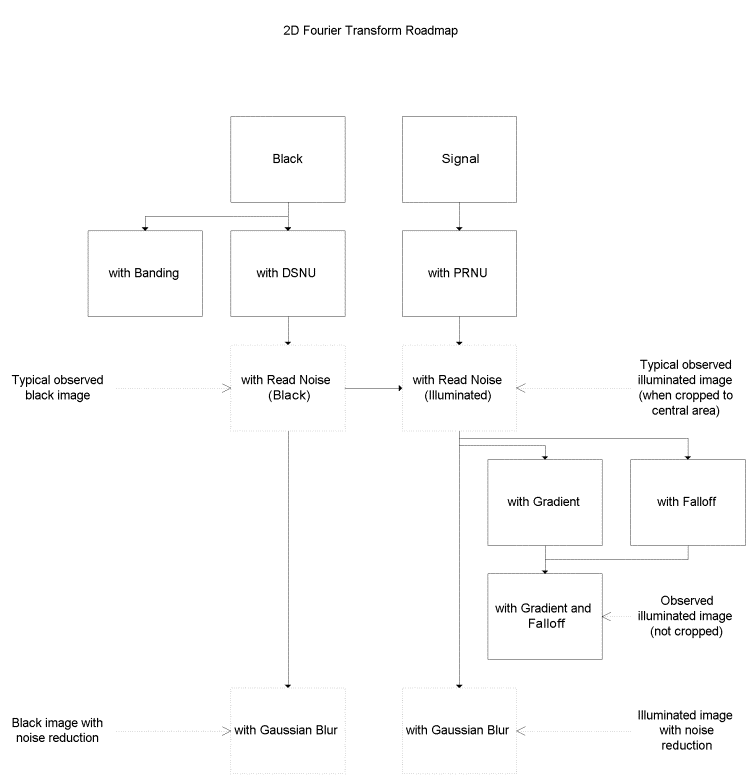
Black

With a hypothetic perfect sensor a black frame and corresponding 2D FT would look like this:

Not too exciting.

Now let's add some randomly placed Dark Signal Non-Uniformity (DSNU):

DSNU arises from the fact that not every pixel starts at exactly the same zero.
DSNU is a form of Fixed Pattern Noise (FPN).

Now we add read noise:

Read noise arises principally from the electronics used to read the value of the pixel (hence the name).
This represents what we might reasonably expect to see from a well behaved sensor.
(Although non-DSNU FPN is not unusual and often presents as horizontal or vertical streaks.
Also, on some sensors, on chip Phase Detect Auto Focus (PDAF) may form a visible pattern.)

Noise Reduction

We are not expecting to see noise reduction in our raw image; but it happens.
Noise reduction, hot pixel suppression, and other signal processing share the same general characteristic.
They all re-compute a pixel value based on neighboring pixels.

So to simulate this effect I added a small Gaussian Blur to the typical black image:

I boosted the contrast on the 2D FT to make the effect more obvious.
This round "sphere-like" effect is an important feature to remember.

Signal

Black images are interesting but I also frequently analyze evenly illuminated images.
So here's what Signal alone would look like:

Since this is just a signal and it's associated Photon Noise it's not too exciting.

Now let's add some randomly placed Photo-Response Non-Uniformity (PRNU):

PRNU is another form of FPN. This results is still pretty uninteresting.

To get something representative of what we can observe, let's add in the DSNU and read noise:

Still not very exciting; but this is what we would expect from a well behaved sensor.

Noise Reduction Revisited

Here's what happens if we apply a Gaussian blur to the signal image:

Once again the tell-tail circle sign that some sort of nearest neighbor signal processing has occurred.

Gradients and Falloff

The manufacturing process can result in a small gradient on the sensor.
We can also get a gradient if our image collection is imperfect.
Here's what the signal image with a gradient looks like:

Well, that's something new.
This cross pattern happens when the left/right or top/bottom edges of the image don't match.
Note the horizontal gradient is stronger than the vertical; and the cross is wider than it is high.

A more common problem with image collection is light falloff (vignetting).
Applied to the signal image it looks like:

This has the same cross effect as the gradient and also a small white center due to the falloff.

For completeness, let's combine them both:

Note that I made the falloff particularly dramatic to better illustrate the effect.

Banding

The electronics used to read out the value of the pixels can sometimes have a vertical or horizontal pattern.
Here I have rearranged the DSNU data from above into vertical bands:

This banding image has exactly the same statistical characteristics as the previous DSNU image shown here for comparison:

So statistically we can't distinguish banding from DSNU.
Banding acts like spatially correlated DSNU even though the origin is the external electronics and not the pixel.
When the pattern of banding remains constant from frame to frame then it is Fixed Pattern Noise (FPN).

Conclusion

We have seen a number of synthetically generated images and their corresponding 2D FTs.
Now we have a good idea of how to interpret patterns in a 2D FT.

We know that a uniform FT with a white center is ideal.
We know that a cross is probably the result of a gradient, falloff, or banding.
We know that a slightly enlarged white center is probably from a strong falloff.
And we know that a large circular pattern is the signature of signal processing such as noise reduction.

There are other interesting case that I did not cover here but you now have the tools to understand their 2D FT.
These cases includes visible bonds along the center of large sensors (which may comprise of two pieces of silicon that are bonded together), visible on chip PDAF, etc.