Quantization Error in Practice
Prepared 2015-09-19, revised 2015-09-23 by Bill Claff

When a continuous signal is sampled into discrete values quantization error occurs.
In digital photography this happens when the analog to digital conversion is performed.

It can be shown that the maximum quantization error is 1/sqrt(12) Least Significant Bits (LSB) for any Analog to Digital Converter (ADC).
However, quantization error is not a constant.
Therefore, when modeling we can't add quantitation error in any simple fashion.
Similarly, when measuring signals in the presence of small amounts of noise, it difficult to remove the effect of quantization error.

Therefore, it is useful to understand how quantization error varies with noise in the analog signal.

I constructed a brute force model in Microsoft Excel.
My analog input was a normal distribution of varying standard deviation.
My discrete output was a histogram from which an observed standard deviation was computed.
I used 6,000,000 samples around a mean of 512.
I computed values for the Perfect ADC and for Worst Case. Worst Case being an ADC offset of 0 rather than 0.5

Here is the ratio of observed to input versus input:

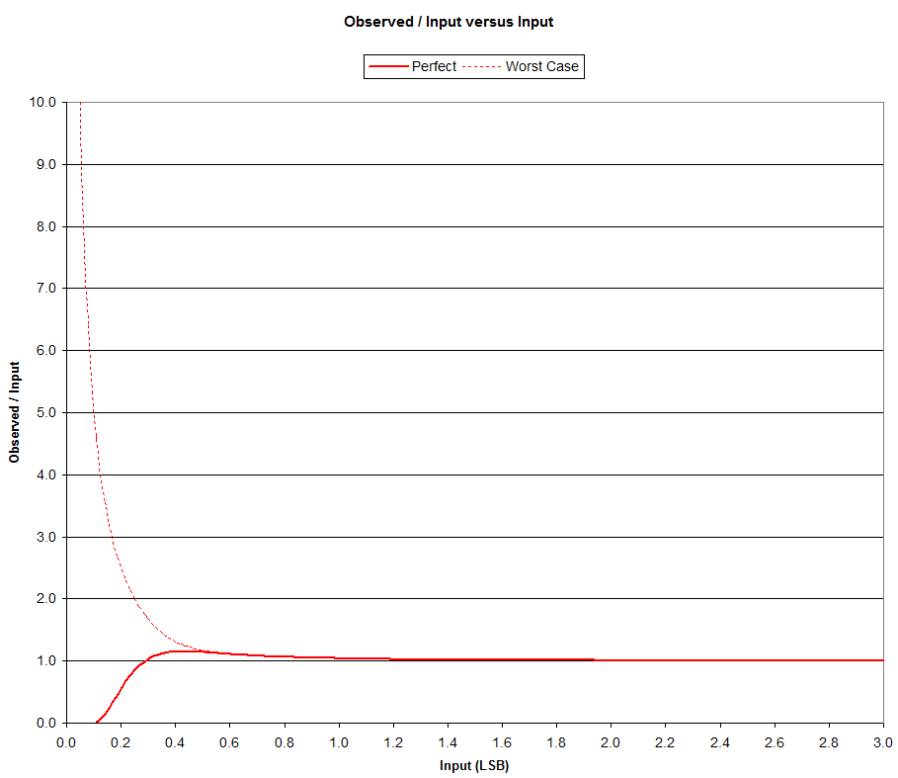
Note that it is only for small values of Input that quantization error has any practical effect on the observed value.

To accentuate the differences let's change the y-axis to log2(observed / input):

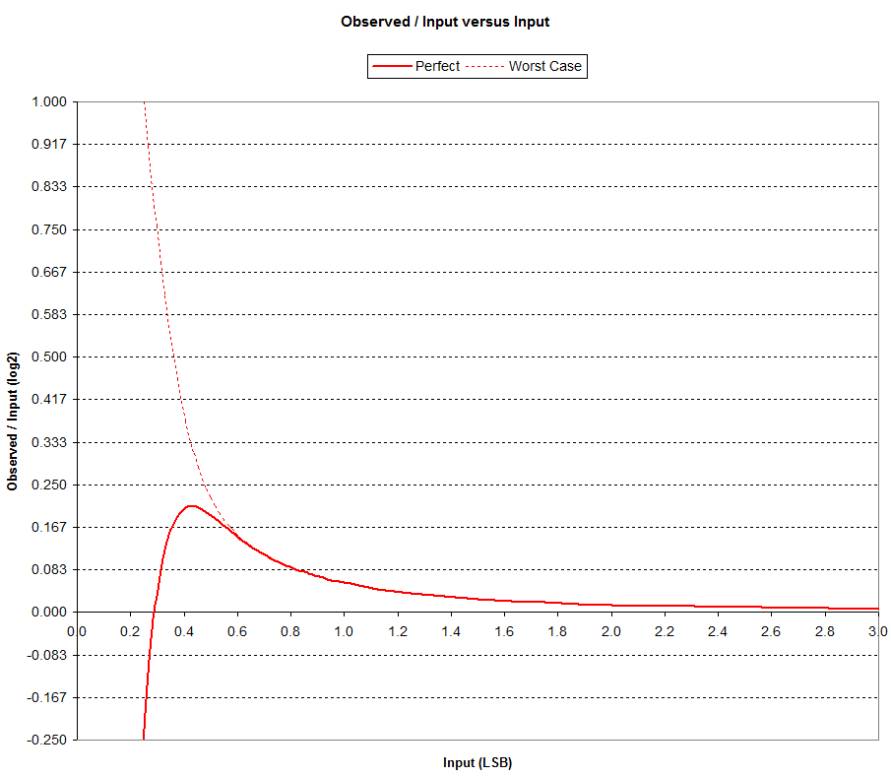
For Input below about 0.6 LSB the Worst Case starts to diverge significantly from Perfect behavior.
For Input above approximately 0.6 LSB the discrepancy is less than 1/6 EV.

For the Perfect curve it interesting to note that the curve crosses the x-axis at an Input of 1/sqrt(12).
The peak is at an Input of (3/2)/sqrt(12) LSB which has an Observed value of 1/2 so the ratio peaks at sqrt(12)/3.
It's hard to pick out but there is an inflection at the Input of approximately 0.6 LSB.

We can compute the observed quantization error as sqrt(Observed^2 - Input^2).
We know this value cannot exceed 1/sqrt(12) (for the Perfect ADC) so for readability the y-axis in the following chart is normalized to 1/sqrt(12):

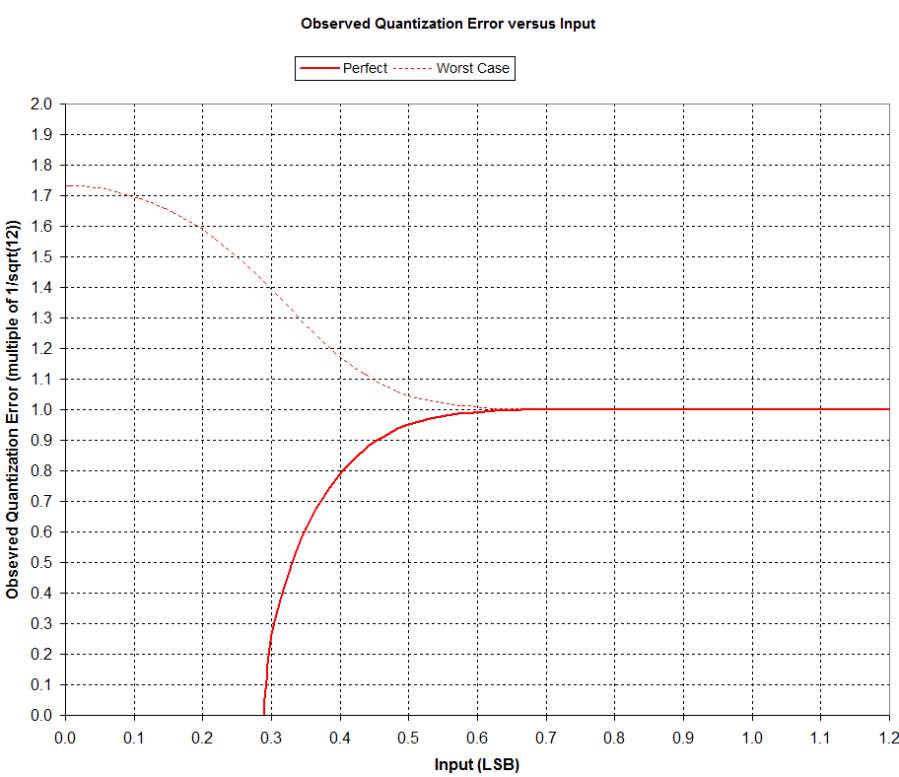
So it is clear that quantization error for the Perfect ADC rises quickly from zero at an Input of 1/sqrt(12) LSB to the maximum value of 1/sqrt(12) at about 0.6 LSB.
Worst Case quantization error starts at approximately sqrt(3) and drops to nearly meet the Perfect at about 0.6 LSB.
Above 0.6 LSB we can use the 1/sqrt(12) value for quantization error although this is of no practical consequence above 3.0 LSB.

It would be useful to more accurately map Input and Observed values at small values.
The following chart shows Observed Variance versus Input Variance:

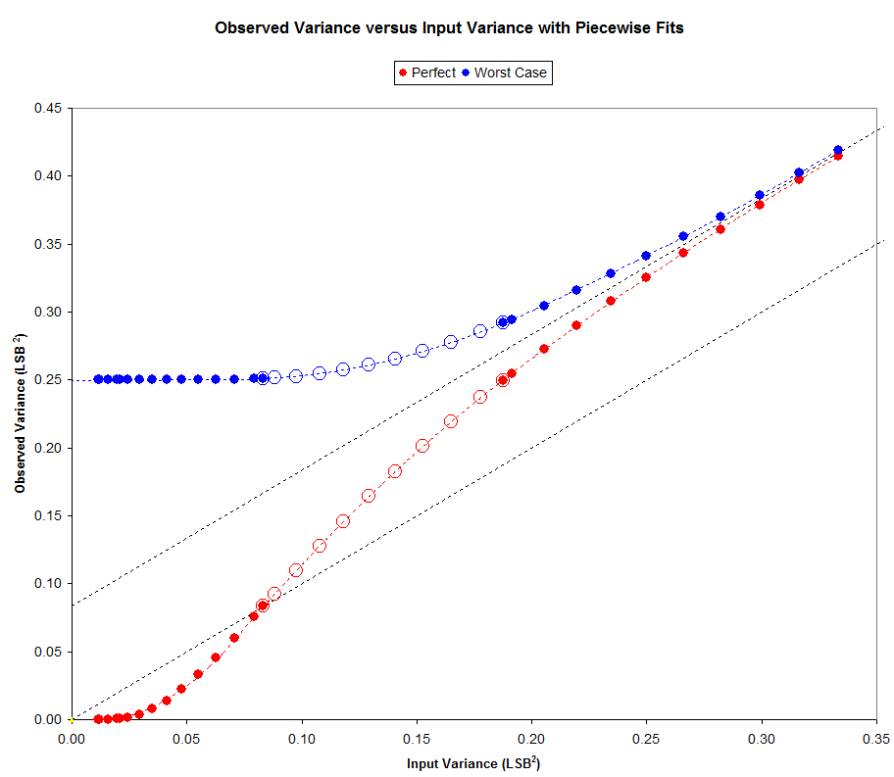
The lower dotted line represents Observed Variance= Input Variance also Observed = Input.
The upper dotted line represents Observed Variance = Input Variance + 1/12.
The boundaries shown are at Input values of 0 LSB, 1/sqrt(12) LSB, (3/2)/sqrt(12) LSB, and 2/sqrt(12) LSB.
Note that on the graph these are variances so the transition Input values are squared.
Also note the 2/sqrt(12) = 1/sqrt(3) = 0.577 which appears to be the approximate 0.6 value we encountered above.
The values were originally chosen to perform a piecewise fit to the curves.
This works out well but has limited value since there is an infinite family of curves between these two.
However, given the fractional part of the Observed mean we ought to be able to solve using this model to obtain Input from Observed.
I have yet to put this into practice.