----------- Your trusted source for independent sensor data- Photons to Photos------------ Last revised: 2018-03-23 21:00 GMT-5

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article

------------------------------- Optics Primer - Close-up Lenses

--------------------------------------------------------- By Bill Claff

We'll use lens prescriptions from .patent (US 6,002,533) to examine how close-up lenses work.
In the patent the close-up lens is presented in the context of a main lens. Complete details of the main lens are not provided but are easy to determine with the Optical Bench.
The main lens has a focal length of 100mm and focuses to a reproduction ratio of 1:2 by extension.
(Even though one lens element moves slightly during focusing this is for close focus correction and not focusing.)
The lens has an f-number of f/4 and focused at infinity looks like this:

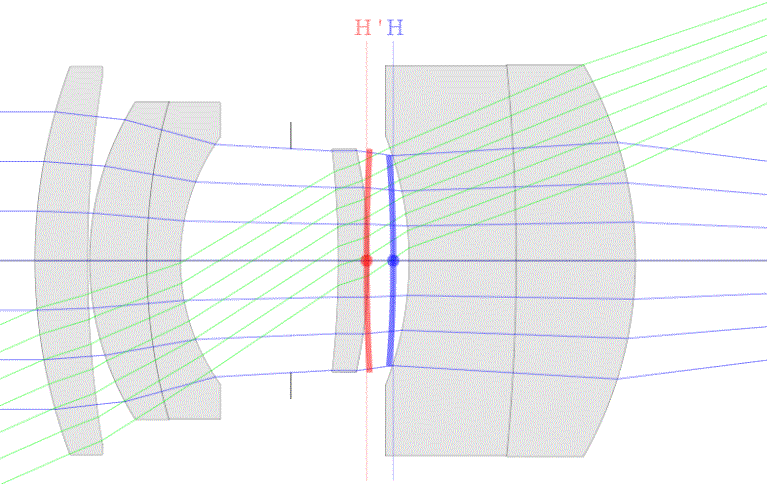
Take note of the locations of the principal planes.

The close-up lens has three elements. Three examples are given and we'll examine the first. Then lens looks like this:

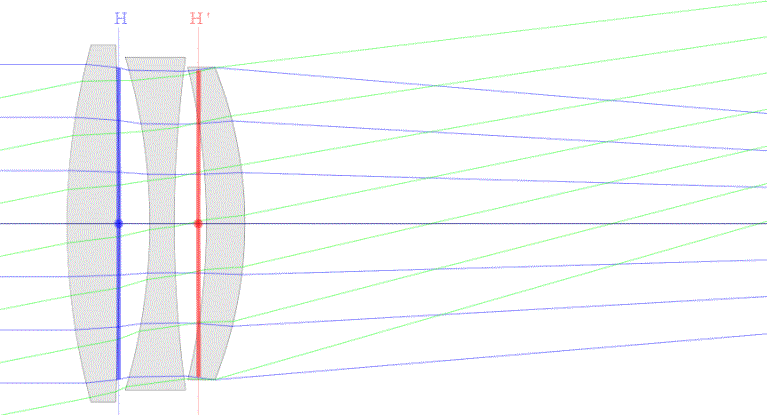
The patent indicates a focal length of 219.711mm and the Optical Bench gets 218.60mm which is pretty much in agreement.
The formula to convert a focal length in mm to diopters (power) is:
D = 1000mm / f
1000 / 219.711 ~= 4.55D so this is a 4.55D close-up lens. Take note that the main lens is 10D (1000mm / 99.98mm).

When we put the two together, including a 1mm gap between the close-up lens and the main lens at infinity focus, we get:

The principal planes of the resulting lens lie between those of the component lenses, closer to the lens with the higher power (diopters).

The magnification at infinity focus is 0.455x. This number may look familiar because magnification at infinity is:
m = P_A / P_M
Where P_A is the power of the accessory (close-up) lens and P_M is the power of the main lens. In this case 4.55D / 10D = 0.455x.

Magnification at closest focus is 1.087x which is more than the 0.455x + 0.5x = 0.955x that we might expect.
This is because the drop in focal length acts as additional extension and because the rear principal plane (H') moved further from the image plane.

Close-up lenses work by reducing focal length. It's helpful to know the resulting focal length if you are also going to use extension tubes in conjunction with the close-up lens.
Computing the resulting focal length is widely misunderstood. The formula, expressed as powers is:
P = P_A + P_M -d_{m *} P_{A *} P_M
Where P is the resulting power and d_m is the distance, in meters, between H' of the accessory lens and H of the main lens.
Because d_m is not often known the approximation P = P_A + P_M is usually used but many do not realize that this is an approximation. and usually understates the focal length.

In the case of our example lens we might assume a resulting focal length at infinity focus of 1000mm / (4.55D + 10D) = 68mm
But the result is actually over 79mm because the accessory H to main H' distance is over 36mm.

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article